The Basics of Direct Digital Synthesizers (DDSs) and How to Select and Use Them
Contributed By DigiKey's North American Editors
2019-03-20
As wireless devices proliferate, designers are using increasingly complex and variable waveforms to meet application requirements in terms of data rates, interference mitigation, cost, footprint, and low power consumption. These waveforms require stable RF sources that can be tuned on demand and are both frequency and phase agile. At the same time, the sources must also provide a high degree of signal purity. The solution to this matrix of requirements lies in direct digital synthesizers (DDS).
DDS generates analog waveforms using digital methods, allowing it to take advantage of digital’s programmability and higher levels of integration and lower cost. Additionally, DDS allows a nearly instantaneous change in frequency or phase, making it a primary source for advanced digital modulation techniques such as frequency shift keying (FSK) and spread spectrum, as well as the use of interference mitigation techniques such as frequency hopping. As a result, DDS ICs are rapidly replacing or augmenting traditional phase locked loops (PLLs) and other analog RF sources, while still offering high stability and signal purity.
This article will review the basics of DDS technology and how to specify a DDS IC. It will then introduce some suitable DDS IC solutions and show how to apply them effectively.
How direct digital synthesis works
Digital synthesis is based on a phase accumulator which generates a series of digital states, the value of which increases linearly, forming a numeric ramp. This signal is made periodic and represents the instantaneous phase of the output waveform, from zero to 2p radians. This is the digital input to a lookup table which converts the numeric ramp into a sine wave (Figure 1). While the most common DDS output waveform is the sine wave; ramps, triangle waves, and square waves are also easily generated.
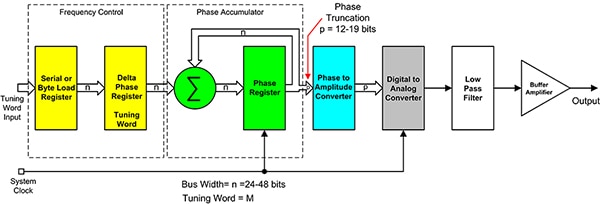
Figure 1: The direct digital synthesizer is based on a phase accumulator which generates the instantaneous phase of a waveform. A lookup table provides the phase to amplitude conversion which is applied to a digital-to-analog converter, producing the desired analog output after filtering. (Image source: DigiKey)
The output of the phase to amplitude lookup table is sent to a digital-to-analog converter (DAC) and is converted into an analog waveform, which is most commonly sinusoidal. Since the input to the DAC is a series of sampled values, the output has quantization steps. These steps produce spectral images at multiples of the sample rate in the frequency domain which are not desired. A low-pass filter, placed after the DAC, suppresses these unwanted spectral responses.
The phase accumulator
The phase accumulator is a modulo N counter that has 2N digital states which are incremented for each system clock input pulse. The size of the increment depends on the value of the tuning word, M, applied to the accumulator adder stage. The tuning word fixes the step size of the counter increment. This will determine the frequency of the output waveform.
The phase accumulator generally has from 24 to 48 bits; at 24 bits there are 224 or 16,777,216 states. This number represents the number of phase values between 0 and 2p radians, or the achievable phase increment. For a 24-bit phase accumulator, the phase resolution is 3.74 E-7 radians. If a larger phase accumulator is used, the phase increment becomes even finer.
One way of visualizing the operation of the phase accumulator is to look at the accumulator operation as a phase wheel (Figure 2).
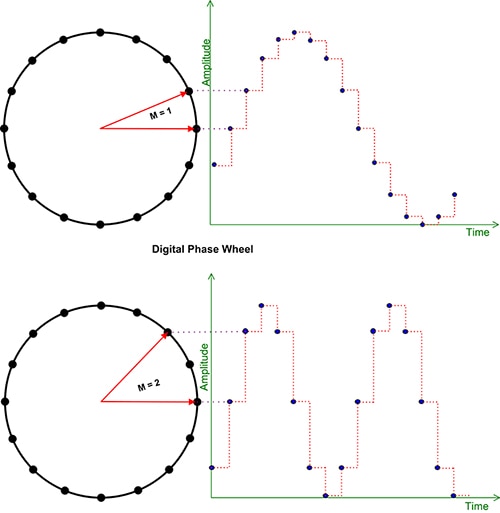
Figure 2: A simplified view of a 16-state phase accumulator operation using a phase wheel to visualize how the tuning word affects the output frequency of the DDS. (Image source: DigiKey)
The accumulator states are periodic and are represented as lying on a circle. Dots on the circle represent all the phase states of the accumulator. In this case, for simplicity, the accumulator has 16 states. If the tuning word is equal to one, as in the top diagram, then the step increment at each clock is one, and all states are selected during the full period.
Projected to the right of the phase wheel is the analog output for each state. As this is a quantized device, the analog output holds its current state until the clock advances the phase wheel to its next state. The output waveform consists of a single cycle of the quantized sine wave containing sixteen values.
In the lower diagram the tuning word value is set to two. With this setting, every other state on the phase wheel is selected. The analog output now consists of two cycles, each with eight amplitudes, giving a total of sixteen states. With the tuning word set to two, the output frequency is now twice the previously obtained value.
The output frequency of the DDS is set by the tuning word value and increases proportionally to the value of the tuning word. The sample rate remains fixed at the system clock rate, and the time between output samples is constant. The output frequency depends on the tuning word increment, so as the tuning word value increases there are fewer steps in each output cycle, thereby increasing the frequency. The tuning word can be increased until there are only two samples per cycle, which brings the DDS output to its Nyquist frequency, or half the system clock rate. Generally, the DDS is limited by design to always have an output frequency that is less than the Nyquist limit.
Along with the system clock frequency, the output frequency of the DDS is also dependent upon the tuning word value, and the length of the accumulator. It is expressed by Equation 1:
![]() Equation 1
Equation 1
Where:
fout is the DDS output frequency
M is the tuning word value
fc is the system clock frequency
N is the length of the phase accumulator
The output of the phase accumulator, which is the instantaneous phase of the output waveform, is used to drive the phase to amplitude converter. The phase to amplitude converter outputs a digital word, the value of which is the amplitude of the sine waveform for the input phase.
Note that the number of bits used to drive the phase to amplitude converter is less than that used for the phase accumulator. This is referred to as phase truncation and is used to reduce the die area and power consumption of the digital stages after the phase accumulator. While it does cause some spurious spectral components, called truncation spurs, they are minimized by careful design.
The reason for the output low-pass filter
The waveforms shown in Figure 2 are harmonic rich due to their stepped character. As a result, a low-pass filter is required to remove these spectral harmonics, as well as other spurious frequency responses resulting from other processes within the DDS.
For example, the DDS output spectrum for a device clocked at fc with an output frequency of less than fc/2 is shown in Figure 3. The output spectrum shows the output spectral line, fout, along with its image frequencies above and below the clock frequency, and all of its harmonics up to and past the third.

Figure 3: The spectral view of a DDS with a system clock frequency of fc and an output frequency of fout showing the output frequency components up to the third harmonic of the clock. (Image source: Analog Devices)
The DDS output frequency range is from 0 Hz to the Nyquist limit at fc/2. The sin(x)/x shaping is due to the quantized signal in the time domain, as shown in Figure 2. Zeros of the sin(x)/x function occur at the clock frequency and at all of its harmonics. Amplitude corrections can be applied to cancel the sin(x)/x shaping in order to improve amplitude flatness across the output range.
A low-pass filter with a sharp cutoff above the DDS’s frequency range is applied in order to significantly reduce the amplitude of the spectral components above Nyquist. If the DDS frequency range is extended to the Nyquist frequency, then the filter would require an infinite steep cutoff slope in order to exclude the lower image frequency about the clock frequency, which would overlap the Nyquist frequency. This is one reason that the DDS frequency range is rarely extended to the Nyquist frequency.
Designing with commercial DDS ICs
There is much to consider when selecting and using a DDS. First, consider the necessary functionality for the applications; the frequency range required, amplitude and offset range, wave shape, resolution, and modulation capability. Signal purity is generally a factor in selecting a signals source. Spurious free dynamic range (SFDR), total harmonic distortion (THD), and phase noise are the key specifications, as is power consumption, especially in mobile applications.
A good example of a low-power DDS is Analog Devices’ AD9834BRUZ-REEL7 (Figure 4). This device is controlled by a three-wire serial interface, consuming only 20 milliwatts (mW) from a 3 volt supply. It can output sine, ramp, and square wave functions, and has a maximum clock frequency of 50 megahertz (MHz), shown in the figure as the digital clock input MCLK. Based on the Nyquist discussion earlier, that clock frequency means it can output waveforms up to 25 MHz.
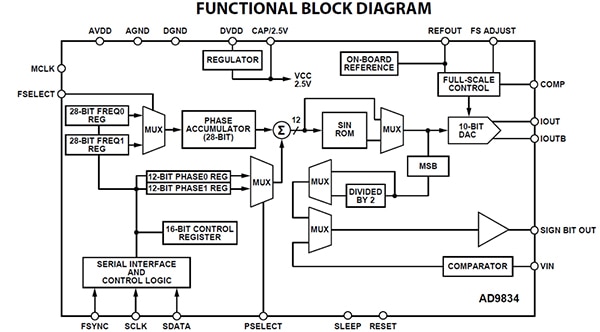
Figure 4: The internal functional diagram of an Analog Devices AD9834 low-power DDS. The device consumes 20 mW from a 3 volt supply and can produce sine, ramp, and square wave functions up to 25 MHz. (Image source: Analog Devices)
The phase accumulator has a length of 28 bits, yielding a frequency resolution of 0.186 Hz at a clock frequency of 50 MHz. The phase noise also depends on the quality of the MCLK input and is shown as a function of an offset from the carrier (Figure 5). In the case of the AD9834, the phase noise is -120 dBc/Hz at a 1 kHz offset from the carrier for an FOUT of 2 MHz and an MCLK of 50 MHz.

Figure 5: The phase noise depends upon the quality of the MCLK and is shown as -120 dBc/Hz at a 1 kHz offset from the carrier for an FOUT of 2 MHz and an MCLK of 50 MHz. (Image source: Analog Devices)
The built-in DAC has a resolution of 10 bits and the narrowband SFDR is typically better than -78 dB.
Features of the AD9834 include dual frequency and phase registers to support both frequency and phase modulation. Also, the sine read-only memory (ROM) can be bypassed to drive the DAC using the phase accumulator output to produce a ramp function. The sign bit is available at an output pin to supply a square wave for clock generation.
To help with the design process, it’s often the case that vendors provide good selection tools to simplify the task. The AD9834 DDS is supported by Analog Devices’ ADIsimDDS, an online, interactive design tool which lets designers evaluate various configurations including output frequencies, tuning words, and reference clocks (Figure 6).

Figure 6: The ADIsimDDS interactive design tool from Analog Devices lets designers experiment with various DD configurations and filtering options. (Image source: Analog Devices)
The ADIsimDDS program starts with the selection of a specific DDS product, in this case the AD9834. The user enters the system clock frequency and desired output frequency, and the program calculates the tuning word for the phase accumulator. A frequency domain display shows the spectrum of the DDS output including the output signal, harmonics, DAC images, clock harmonics, and clock images. A filter simulator can be applied to the DDS output to see the effects of various filters on the output spectrum.
If the design requires higher performance and frequencies, the Analog Devices AD9952YSVZ-REEL7 has a maximum clock frequency of 400 MHz, and can produce sinusoidal signals up to 200 MHz with lower phase noise and an SFDR specified at >80 dB at 160 MHz (±100 kilohertz (kHz) offset) AOUT. Comparing directly to the AD9834, its narrowband SFDR is typically -70 dB at 20 MHz, but of course this is frequency dependent.
The AD9952 doesn’t use an MCLK input. Instead it has a built-in clock oscillator with an associated PLL multiplier that can multiply the clock by factors of 4 to 20 times using a single external crystal (Figure 7). Having its own internal system clock of (up to 400 MSPS) allows the DDS to achieve its low phase noise of ≤ -120 dBc/Hz @ 1 kHz offset.
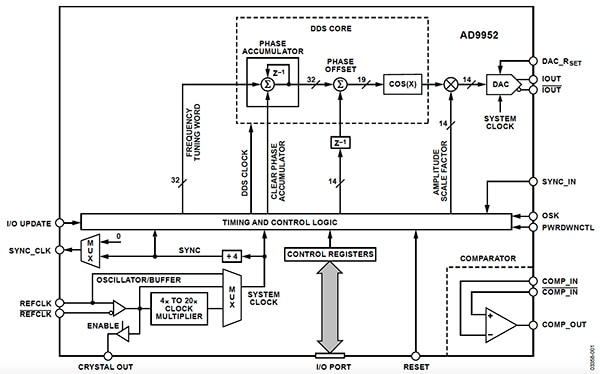
Figure 7: The AD9952 takes the external crystal’s input and generates its own internal system clock to better control the conditions necessary for higher performance, such as lower phase noise. (Image source: Analog Devices)
The AD9952 also features a 32-bit phase accumulator depth and a 14-bit DAC. The DDS is controlled via a serial interface.
For a wider frequency range there is the Analog Devices AD9957BSVZ-REEL, which supports clock rates up to 1 gigahertz (GHz) with output frequencies to 400 MHz for advanced communications applications. Utilizing a 32-bit phase accumulator and a 14-bit high-speed DAC, this device is intended as a quadrature modulator and generates both in-phase (I) and quadrature (Q) components controlled by eight phase/frequency registers. These are used to produce a quadrature modulated data stream at the output. An optional inverse SINC (sin(x)/x) filter is available to compensate for the sin(x)/x shaping discussed previously.
These are three examples of commercially available DDS integrated circuits spanning from simple to complex signal generation tasks.
Conclusion
With designers constantly challenged to improve wireless system performance, size, cost, and power consumption, DDSs are shown to be a good option. They bring digital stability, agility, and repeatability to signal generation, offering multiple output waveforms and advanced modulation capability, including frequency and phase hopping. As they become part of the designer’s toolkit, vendors are also simplifying their selection and integration through the use of advanced tools that shorten the design process.

Disclaimer: The opinions, beliefs, and viewpoints expressed by the various authors and/or forum participants on this website do not necessarily reflect the opinions, beliefs, and viewpoints of DigiKey or official policies of DigiKey.







