Un CAN peut-il être simplement un générateur de nombres aléatoires ?

Quel est le niveau de performances d'un CAN ? Cette question ne porte pas sur le nombre de bits de résolution dont il dispose. Il peut être surprenant d'apprendre qu'un CAN 16 bits ne fournit pas toujours 16 bits d'informations utiles ! « De nombreux CAN 16 bits fonctionnent en réalité comme des CAN 7 bits et des générateurs de nombres aléatoires 9 bits », explique Mike Stone dans « Choosing an ADC ». Cet article montre comment déterminer si un CAN génère plus de nombres aléatoires que de nombres utiles, et présente quelques méthodes simples pour réduire le caractère aléatoire.

Considérons une configuration simplifiée : un CAN mesurant la tension d'une photorésistance. Si le CAN 12 bits dans la Figure 1 (avec V_FS = 3,3 V) indique une valeur de 2048, cela signifie-t-il que la tension sur la photorésistance est de 1,65 V ?

Figure 1 : Configuration simplifiée d'un CAN pour mesurer la tension d'une photorésistance. (Source de l'image : Nathan Jones)

Non, pas vraiment ! Pour le démontrer, prenons un deuxième échantillon, puis un troisième, et, en fait, prenons 100 000 échantillons et traçons les résultats. Nous observons une distribution des valeurs CAN (Figure 2). Si rien n'a changé dans la configuration, alors n'importe laquelle de ces valeurs peut être la tension réelle de la photorésistance, la valeur moyenne de tous ces échantillons étant la plus probable.

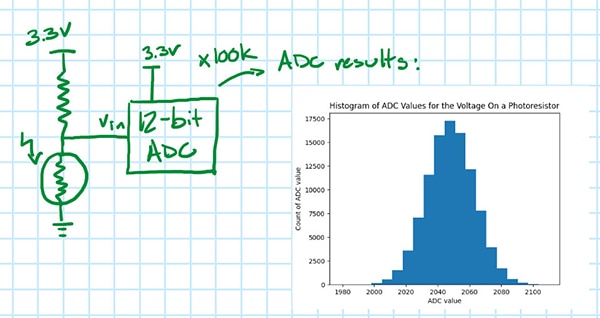Figure 2 : L'encart montre l'histogramme des valeurs CAN pour 100 000 échantillons de tension de photorésistance. (Source de l'image : Nathan Jones)

Cela soulève une autre question. Une partie de ces variations pourrait-elle être due à des variations réelles dans le signal d'entrée ? Oui, c'est possible. Pour le vérifier, le diviseur résistif est remplacé par une référence de tension (Figure 3) avec un niveau de bruit connu et l'expérience est renouvelée.

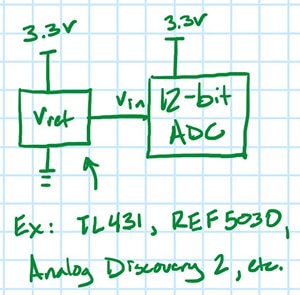Figure 3 : Nouvelle configuration de test avec une référence de tension à la place du diviseur résistif. (Source de l'image : Nathan Jones)

Idéalement, la référence de tension utilisée doit avoir un niveau de bruit inférieur à 1/3 du niveau de bruit attendu dans le CAN (par exemple, si le CAN est supposé présenter ±1 LSB de bruit [ce qui serait ±0,8 mV en utilisant le CAN dans l'exemple ci-dessus], alors idéalement la référence de tension doit avoir un niveau de bruit inférieur à 0,27 mV_pp). Si c'est le cas, alors on s'attend à ce que tout le bruit mesuré provienne du CAN, en se basant sur le fait que le bruit non corrélé s'additionne en quadrature (Équation 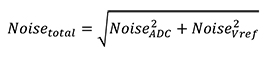1).

 [1]

Si Noise_Vref=Noise_ADC/3 alors Noise_total=1,054 × Noise_ADC. Cela signifie que la référence de tension ne contribue qu'à 5,4 % du bruit total, soit une quantité négligeable. S'il s'avère que la référence de tension présente plus de bruit que 1/3 du bruit du CAN, pensez à soustraire sa contribution de l'écart-type mesuré (Équation 2).

 [2]

Comment connaître le niveau de bruit d'une source de tension

Le moyen le plus simple est de consulter la fiche technique. Voici un exemple de la fiche technique du REF5030 de Texas Instruments, montrant que ce composant a un niveau de bruit de 9 μV_pp.

Figure 4 : Extrait de la fiche technique du REF5030 présentant les spécifications de tension de bruit de sortie. (Source de l'image : Texas Instruments)

Si la fiche technique n'indique pas de niveau de bruit (ou si vous souhaitez juste vérifier sa valeur), mesurez-le simplement avec un oscilloscope, après avoir déterminé le bruit de fond de l'oscilloscope. Pour ce faire, il suffit de connecter l'une des entrées de l'oscilloscope à la terre et de mesurer la valeur efficace des variations du signal observé. La Figure 5 illustre le résultat de cette opération avec un oscilloscope Analog Discovery 2 (AD2), démontrant que le bruit RMS est d'environ 0,9 mV. Il est intéressant de noter que cette valeur diminue (jusqu'au niveau des µV) si la base de temps est augmentée au-delà de 8 µs/div, probablement parce que l'AD2 utilise le suréchantillonnage et la décimation pour accroître sa résolution effective.

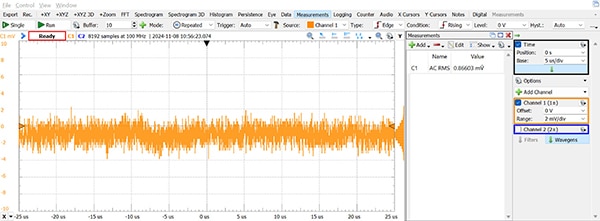Figure 5 : Graphique du niveau de bruit de fond de l'oscilloscope Analog Discovery 2. (Source de l'image : Nathan Jones)

Lorsque la source de tension est mesurée, toutes les variations du signal de l'oscilloscope sont le résultat du bruit combiné de la source de tension et de l'oscilloscope. Tant que ces sources de bruit ne sont pas corrélées (ce qui est le cas), alors Noise_measured=√(Noise²_Scope+Noise²_Vref) et Noise_Vref=√(Noise²_Measured-Noise²_Scope), comme ci-dessus. Lors de la mesure d'un signal de 2 V_CC généré par l'AD2, un bruit de 1,2 mV a été constaté (Figure 6).

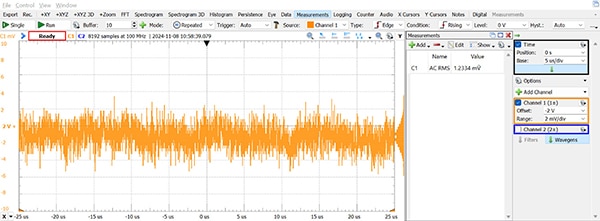Figure 6 : Ce tracé d'un signal de 2 VCC indique que le bruit de l'oscilloscope était de 1,2 mV. (Source de l'image : Nathan Jones)

Cela indique que le générateur de signaux sur l'AD2 présente également un niveau de bruit d'environ 0,9 mV. Ce niveau est suffisamment bas pour tester un CAN 10 bits (0,9 mV est juste inférieur à 1/3 d'un LSB pour un CAN 10 bits avec une mesure pleine échelle de 3,3 V). Pour tout CAN à résolution plus élevée, ce bruit doit être pris en compte dans les mesures.

Figure 7 : L'encart montre le nouvel histogramme des valeurs CAN pour 100 000 échantillons de tension de photorésistance avec la référence de tension. (Source de l'image : Nathan Jones)

C'est beaucoup mieux ! Notez maintenant comment le deuxième histogramme (Figure 7) ne va que jusqu'à 2052 sur l'axe des x (la distribution sur ce graphique [Figure 8] a un écart-type de 1 LSB), alors que le premier graphique allait jusqu'à 2100 (avec un écart-type de 15 LSB). C'est ce que l'on appelle le test par histogramme DC pour un CAN et l'écart-type indique effectivement la quantité de bruit présente dans le CAN : chaque fois qu'une valeur est mesurée avec le CAN, il n'y a que 68 % de chances que la valeur réelle sur la broche analogique se situe réellement à ±1 écart-type de cette valeur, mais il y a 99,7 % de chances que la valeur réelle se situe à ±3 écarts-types de cette valeur.

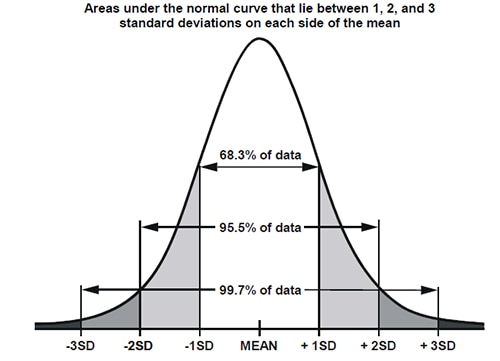Figure 8 : Courbe de distribution avec écarts-types. (Source de l'image : https://i.sstatic.net/jkMDV.png)

La conversion de cet écart-type de LSB en volts donne le bruit référencé à l'entrée pour le CAN (Équation 3).

 [3]

Si le CAN présente si peu de bruit que tous les codes CAN tombent dans un seul compartiment (bin), essayez de réduire la tension de référence CAN. Le niveau de bruit reste le même mais prend plus de codes CAN qu'auparavant, ce qui permet de trouver une valeur appropriée pour le bruit référencé à l'entrée.

La résolution effective et la résolution de code en l'absence de bruit (NFCR) d'un CAN représentent dans quelle mesure ce bruit limite la résolution du CAN. Elles sont calculées en divisant la plage complète de codes CAN en compartiments dont la largeur est égale à 1 (Équation 4) ou à 6,6 écarts types (Équation 5).

 [4]

 [5]

En substance, il y a moins de bits réels dans le résultat car il y a un risque croissant que les derniers bits du résultat CAN soient erronés ou bruyants.

Une version légèrement plus simple du test par histogramme DC consiste à mettre à la terre l'entrée du CAN, puis à créer un histogramme (Figure 9) des résultats du CAN, comme cela a été fait pour l'oscilloscope.

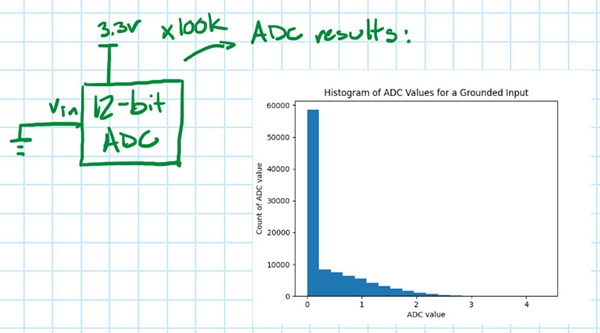Figure 9 : L'encart montre l'histogramme des échantillons de tension de sortie CAN avec l'entrée mise à la terre. (Source de l'image : Nathan Jones)

L'écart-type de cet histogramme est également une mesure du bruit CAN (moins les contributions du bruit dans la tension de référence CAN, qui n'affecte pas les mesures de 0 V), mais il est optimistement faible. Il est probable que le CAN signale les valeurs inférieures à 0 V comme étant simplement 0, de sorte que seule la moitié de la véritable distribution du bruit est visible. Dans ce cas, le bruit CAN peut être approximé si l'on suppose que la distribution est symétrique par rapport à sa valeur moyenne, en changeant suffisamment de valeurs médianes en nombres négatifs pour que la distribution devienne symétrique, puis en calculant l'écart-type de cette distribution (Figure 10).

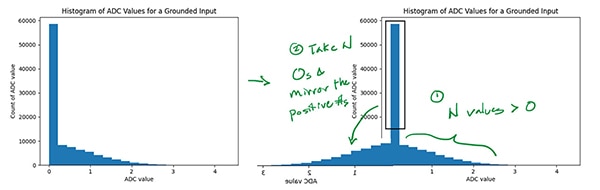Figure 10 : Image miroir de l'histogramme de la Figure 9 pour approximer le bruit CAN. (Source de l'image : Nathan Jones)

Alors, que faire, face à tout ce bruit ? Si la résolution du CAN est toujours dans les limites des exigences du projet (quelle chance !), n'oubliez pas que chaque mesure CAN comporte une part d'incertitude :

• Lorsque vous comparez deux valeurs CAN, ne les considérez comme équivalentes que si elles sont à moins de 6,6 σ l'une de l'autre (pour une confiance de 99,7 % dans la comparaison) ou si elles sont à moins de σ l'une de l'autre (pour une confiance de seulement 68 %).
• Lorsque vous comparez une valeur CAN à un seuil, ajoutez une certaine hystérésis à la comparaison du seuil (comme le fait un thermostat) pour éviter que le système embarqué ne se redéclenche au-dessus et en dessous de ce seuil uniquement en fonction du bruit.

S'il s'avère que le CAN ne répond plus aux exigences du projet, il existe quelques moyens simples d'améliorer ses performances. Côté matériel, il s'agit notamment de procéder comme suit :

• Utiliser une référence à plus faible bruit (comme le REF5030 de Texas Instruments ou le TL431 d'EVVO) pour AVCC et AREF
• Garantir une diaphonie minimale entre les signaux analogiques et numériques sur le circuit imprimé
• Désactiver le processeur pendant les conversions CAN (si le microcontrôleur le prend en charge), pour réduire le bruit numérique

Côté logiciel, il est possible de suréchantillonner le signal d'entrée (c'est-à-dire de prendre la moyenne de N échantillons) pour réduire le bruit, bien que cela réduise clairement la fréquence d'échantillonnage maximum. (En fait, une technique appelée « suréchantillonnage et décimation » peut être utilisée pour augmenter la résolution du CAN d'une quantité proportionnelle au nombre de fois où l'entrée est suréchantillonnée.)

Supposons que l'écart-type d'un test par histogramme DC pour la configuration initiale est de 1 LSB. Si le CAN indique 2048, cela signifie-t-il alors (avec une probabilité de 68 %) que la valeur réelle est de 1,650±0,008 V (Figure 11) ?

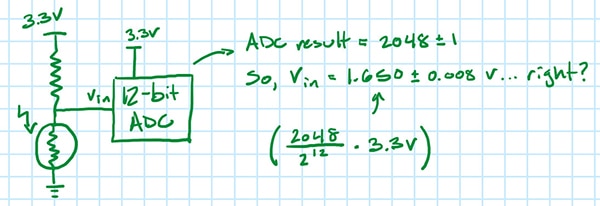Figure 11 : En supposant que l'écart-type de la configuration de la Figure 1 est de 1 LSB et que la sortie CAN est de 2048, la tension d'entrée réelle est-elle de 1,650±0,008 V ? (Source de l'image : Nathan Jones)

On se rapproche, mais ce n'est toujours pas ça ! En effet, tous les CAN ont du mal à mesurer un signal d'entrée changeant rapidement à une certaine fréquence, ce qui se traduit par des mesures imprécises (c'est-à-dire du bruit). Étonnamment, la fréquence à laquelle cela se produit peut être bien inférieure à la fréquence d'échantillonnage maximum du CAN ! Cela signifie qu'un CAN 12 bits avec une fréquence d'échantillonnage de 1 Méch./s peut ne pas avoir réellement une résolution de 12 bits pour les signaux d'entrée proches de 500 kHz. La résolution de ce CAN peut tomber à 6 bits ou moins lorsque la fréquence du signal d'entrée est aussi élevée. Si vous essayez de mesurer un signal supérieur à 10 Hz sur la photorésistance, il se peut que le CAN n'ait pas une résolution de 12 bits.

Pour déterminer dans quelle mesure la résolution du CAN résiste aux fréquences d'entrée plus élevées, envoyez un signal de référence (ici, une onde sinusoïdale) et mesurez la correspondance des valeurs CAN avec ce signal de référence (Figure 12). (L'onde sinusoïdale est-elle de qualité suffisante ? Cette question sera abordée une fois la procédure de réalisation du test révélée, elle aura alors plus de sens).

Figure 12 : Configuration de test avec une entrée d'onde sinusoïdale de référence. (Source de l'image : Nathan Jones)

Pour l'onde sinusoïdale, il est possible d'utiliser un générateur de fonctions (comme ceux disponibles sur de nombreux oscilloscopes USB), une puce DDS (comme l'AD9834 d'Analog Devices) ou un générateur d'onde sinusoïdale personnalisé (basé sur un oscillateur à pont de Wien ou utilisant un MAX7400 d'Analog Devices pour le filtrage passe-bas d'une onde carrée, par exemple). Il est important de noter que seules les fréquences d'entrée qui ne sont pas des sous-multiples entiers de la fréquence d'échantillonnage doivent être utilisées pour ce test (par exemple, n'utilisez pas une fréquence d'entrée de 1 kHz si la fréquence d'échantillonnage est de 100 kHz). Cela permet d'éviter d'échantillonner par erreur l'onde sinusoïdale aux mêmes endroits à chaque cycle. De plus, pour solliciter au maximum le CAN, réglez l'amplitude de l'onde sinusoïdale d'entrée sur la valeur la plus élevée qui n'écrête pas la sortie (par exemple, un peu moins de 1,65 V pour le CAN dans les exemples ci-dessus).

Après avoir collecté les résultats CAN, les données sont ajustées à une onde sinusoïdale pour calculer l'erreur résiduelle. L'ajustement de l'onde sinusoïdale peut être effectué avec presque n'importe quelle quantité de données, mais pour obtenir des résultats optimaux, il doit y avoir au moins cinq périodes complètes de l'onde sinusoïdale d'entrée. Il est probable qu'il faille initialiser l'algorithme d'ajustement sinusoïdal en lui donnant des estimations initiales pour l'amplitude, la fréquence, le déphasage et le décalage (Figure 13).

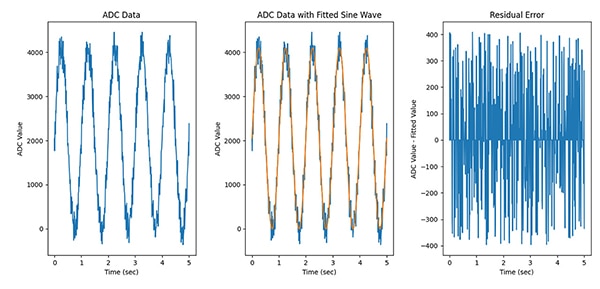Figure 13 : L'erreur résiduelle peut être déterminée à l'aide d'un algorithme d'ajustement d'onde sinusoïdale. (Source de l'image : Nathan Jones)

Ce test est appelé test d'ajustement d'onde sinusoïdale pour un CAN, et la valeur efficace de l'erreur résiduelle est une mesure du niveau de bruit du CAN à cette fréquence d'entrée spécifique. Aux basses fréquences, le bruit RMS devrait correspondre au bruit référencé à l'entrée du test par histogramme DC, mais à des fréquences plus élevées, il se dégradera presque certainement en raison des sources de bruit dépendant de la fréquence mentionnées ci-dessus.

La valeur de bruit RMS du test d'ajustement d'onde sinusoïdale peut être utilisée pour calculer le nombre de bits effectif (ENOB) du CAN (Équation 6), qui est le nombre de bits d'un CAN idéal dont la seule source de bruit, la distorsion de quantification, a la même valeur efficace que le bruit dans le CAN.

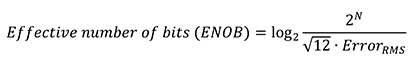 [6]

Cette valeur est spécifique à la fréquence du signal d'entrée qui a été utilisé. Pour obtenir une image plus complète du CAN, ce test doit être répété à des fréquences allant jusqu'au signal d'entrée d'intérêt le plus élevé, ou jusqu'à la moitié de la fréquence d'échantillonnage maximum. Il se peut que le bruit augmente considérablement (et que l'ENOB diminue considérablement !) à des fréquences bien inférieures à la moitié de la fréquence d'échantillonnage maximum ! Par exemple, cette série exacte de tests a été effectuée sur le CAN d'un STM32F042K6 de STMicroelectronics et les résultats ont été représentés graphiquement (Figure 14).

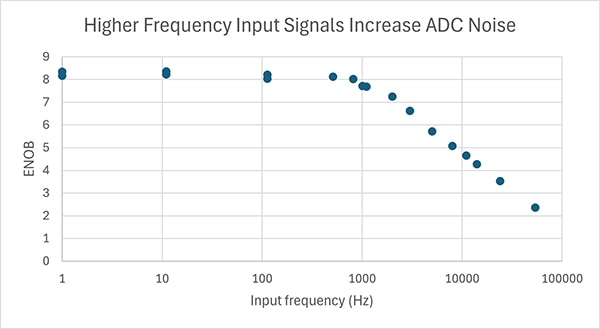Figure 14 : Test de bruit de fréquence pour un CAN dans un microcontrôleur STM32F042K6. (Source de l'image : Nathan Jones)

Même si le CAN sur le microcontrôleur STM32F042K6 peut échantillonner à 1 MHz, la résolution chute au-dessus de 1 kHz. Si l'objectif était de mesurer un signal de 10 kHz avec ce CAN, il n'y aurait plus qu'une résolution d'environ 5 bits à ce stade ! (Notez également que l'ENOB maximum est d'environ 8,3 ; cela est dû à environ 10 LSB de bruit même à CC, ce qui réduit d'emblée la résolution effective du CAN de 12 bits à environ 8,7 bits. Ces tests ont été réalisés sur une carte de développement Nucleo-F042 non modifiée de STMicroelectronics. Les résultats seraient bien meilleurs si l'une des techniques mentionnées ci-dessus était utilisée [« Alors, que faire, face à tout ce bruit ? »].)

Comment connaître le niveau de bruit d'une onde sinusoïdale

Comme pour la référence de tension, si le niveau de bruit de l'onde sinusoïdale est supposé a priori (c'est-à-dire s'il n'est pas indiqué dans une fiche technique), il est alors nécessaire de le mesurer avec un oscilloscope. L'utilisation de la technique d'ajustement d'onde sinusoïdale décrite précédemment permet de caractériser le bruit du générateur d'onde sinusoïdale.

1. Tout d'abord, déterminez le bruit de fond de l'oscilloscope en connectant son entrée à la terre et en calculant la valeur efficace de la sortie (comme décrit précédemment dans la section « Comment connaître le niveau de bruit d'une source de tension »).
2. Ensuite, mesurez la sortie du générateur d'onde sinusoïdale, ajustez les résultats à une onde sinusoïdale parfaite et calculez la valeur efficace des résidus. Utilisez enfin l'Équation 2 pour déterminer le bruit du générateur d'ondes sinusoïdales (en utilisant le bruit de fond de l'oscilloscope comme approximation de son bruit CA).

Idéalement, le niveau de bruit de l'onde sinusoïdale est inférieur à 1/3 du niveau de bruit attendu du CAN (en d'autres termes, l'onde sinusoïdale est « spectralement pure »), ce qui rend sa contribution au bruit mesuré négligeable. Si le niveau de bruit de l'onde sinusoïdale est plus élevé, n'oubliez pas de le soustraire du bruit mesuré obtenu par le calcul des valeurs efficaces de l'erreur résiduelle.

Ce test doit être répété pour chaque fréquence d'entrée destinée à être utilisée pour tester le CAN (même le générateur d'ondes sinusoïdales peut avoir des sources de bruit dépendant de la fréquence !).

Que faire face à tout ce bruit ? Tout d'abord, il est recommandé de placer un filtre passe-bas (LPF) entre la source de signal et le CAN, avec une fréquence de coupure juste au-dessus du signal d'intérêt le plus élevé, pour aider à limiter le bruit haute fréquence (il s'agit d'une bonne pratique, en général, pour tout système d'acquisition de données). Si le signal de fréquence d'intérêt le plus élevé est inférieur au point d'inflexion dans le graphique de la valeur ENOB par rapport à la fréquence d'entrée, il n'y a alors pas de perte de résolution. Si l'on essaie de mesurer des signaux au-dessus de ce point d'inflexion, il existe quelques possibilités d'améliorer la résolution à des fréquences plus élevées, notamment :

• S'assurer que l'impédance de sortie du dispositif connecté à la broche analogique est très faible, en insérant éventuellement un amplificateur opérationnel pour la mise en tampon
• Ajuster l'horloge CAN ou son temps d'échantillonnage/de maintien à la vitesse la plus élevée possible, tout en laissant au condensateur interne suffisamment de temps pour se charger
• Utiliser une source d'horloge CAN à faible gigue et configurer le système pour prendre des échantillons CAN à intervalles réguliers

À moins qu'un signal dans une bande de fréquences très étroite ne soit l'objectif, la chose la plus simple à faire ensuite est de supposer que les signaux d'entrée réels ont un contenu de fréquence égal de CC à la fréquence de coupure du LPF, et donc que le bruit RMS dans chaque mesure CAN est le bruit RMS moyen mesuré à l'aide du test d'ajustement d'onde sinusoïdale de CC à la fréquence de coupure. Si l'on souhaite mesurer des signaux à large bande jusqu'à 10 kHz à l'aide du STM32F042K6 décrit précédemment, il est préférable de fonctionner comme si le CAN n'avait qu'une valeur ENOB d'environ 6 bits pour chaque mesure. Cette valeur peut très bien être inférieure à celle déterminée à l'aide du test par histogramme DC, ce qui indique qu'il y a moins de certitude dans chacune des mesures CAN s'il existe une possibilité qu'elles aient un contenu de fréquence plus élevé.

L'hypothèse suivante à prendre en compte est l'ajout d'un LPF entre le capteur et le CAN de sorte que le bruit RMS de CC à la fréquence de coupure ne soit que de ±1 LSB. Si le CAN indique 2048, cela signifie-t-il alors (avec une probabilité de 68 %) que la valeur réelle est de 1,650 ±0,008 V (Figure 15) ?

Figure 15 : L'ajout d'un filtre passe-bas au circuit résulte-t-il en une valeur réelle de 1,650±0,008 V ? (Source de l'image : Nathan Jones)

Aussi fou que cela puisse paraître, ce n'est toujours pas le cas ! Bien que cet article ait effectivement caractérisé le bruit dans le CAN, il n'a pas encore caractérisé son erreur. À l'issue des tests décrits ici, la seule certitude est que deux valeurs CAN sont identiques ou différentes. Cependant, on ne sait pas si un code CAN de 2048 correspond exactement à 1,65 V ou à une autre valeur. Les erreurs de gain, de décalage et de non-linéarité différentielle (entre autres) peuvent signifier que la conversion d'un code CAN en une tension réelle est plus compliquée que l'utilisation de V_in=résultat CAN × V_FS/2^N. Mais c'est un sujet pour un autre article !

Références

1. Characterizing the Raspberry Pi Pico ADC
2. Understanding Data Converters (Texas Instruments)
3. Understand SINAD, ENOB, SNR, THD, THD + N, and SFDR so You Don't Get Lost in the Noise Floor (Analog Devices)
4. The Good, the Bad, and the Ugly Aspects of ADC Input Noise--Is No Noise Good Noise? (Analog Devices)
5. Getting the most out of the SAM D21's ADC (Thea Codes)
6. "Analog-to-Digital Converter Testing" (Kent Lundberg)
7. Dynamic Tests For A/D Converter Performance (Texas Instruments)
8. How to optimize the ADC accuracy in the STM32 MCUs (STM)
9. Enhancing ADC resolution by oversampling (Atmel)
10. Fundamentals of Precision ADC Noise Analysis (Texas Instruments)
11. ADC Gain and Offset Error Calibration on ARM® Cortex®-M0+ Based MCUs (Microchip)
12. Sine wave generation via low-pass filtering a square wave
13. Understanding the impact of digitizer noise on oscilloscope measurements (EE Times)
14. Understanding Effective Number of Bits (Robust Circuit Design)